[iOS] Tìm hiểu về cơ chế giảm tốc của UIScrollView

Thứ Ba, 17/11/2020

Tram Ho

Xin chào mọi người. Trong bài viết này, tôi sẽ cho các bạn biết cơ chế giảm tốc khi cuộn của UIScrollView, và làm thế nào để ta có thể tự implement cơ chế này.

Hiểu cách mà cơ chế cuộn hoạt động sẽ khá là có ích khi ta muốn bắt chước animation của UIScrollView cho một view nào đó khác bằng cách sử dụng UIPanGestureRecognizer.

Cần phải tìm ra phương trình chuyển động để hiểu cách cơ chế cuộn hoạt động. Và khi chúng ta tìm ra, chúng ta có thể tính toán được các thành phần của chức năng cuộn này: thời gian cuộn, vận tốc và vị trí cuối cùng (hình chiếu) sau khi cuộn kết thúc.

Hàm để tính toán hình chiếu (projection) của việc cuộn đã được giới thiệu ở Designing Fluid Interfaces (WWDC18).

// Distance travelled after decelerating to zero velocity at a constant rate.
func project(initialVelocity: Float, decelerationRate: Float) -&gt; Float {
    return (initialVelocity / 1000.0) * decelerationRate / (1.0 - decelerationRate)
}

// Distance travelled after decelerating to zero velocity at a constant rate.

func project(initialVelocity: Float, decelerationRate: Float) -> Float {

return (initialVelocity / 1000.0) * decelerationRate / (1.0 - decelerationRate)

}

Tuy nhiên đây chỉ là hàm của scroll projection. Nó chưa đủ cho hàm tính thời gian hay phương trình chuyển động. Nhưng có thể sử dụng để tham chiếu các tính toán của chúng ta.

Hàm tính vận tốc (velocity function)

Thử đoán xem việc giảm tốc thực hiện như thế nào và DecelerationRate có thể là gì? Trong tài liệu của Apple nói rằng:

A floating-point value that determines the rate of deceleration after the user lifts their finger.

Chúng ta có thể giả định rằng tỷ lệ này cho biết tốc độ cuộn sẽ thay đổi bao nhiêu trong một milli giây (tất cả các giá trị trong UIScrollView được thể hiện dưới dạng milli giây, không giống như UIPanGestureRecognizer).

Nếu ở thời điểm vuốt đi và thả tay ra, chúng ta có vận tốc ban đầu v₀ và chúng ta chọn DecelerationRate.fast, khi đó:

sau 1 milli giây vận tốc sẽ là 0.99 lần v₀
sau 2 milli giây vận tốc sẽ là 0.99² lần v₀
sau k giây, vận tốc sẽ là 0. 99¹⁰⁰⁰k lần v₀

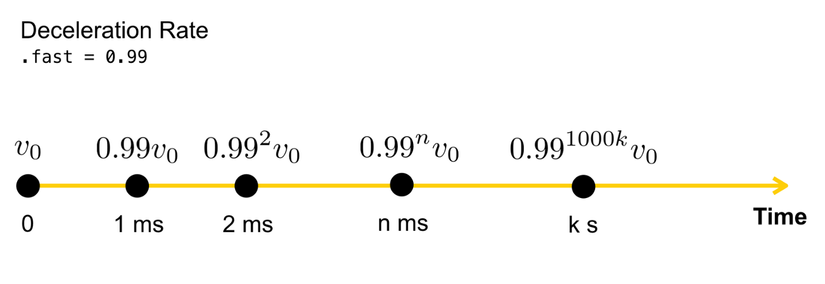
Hiển nhiên mà nói, ta có công thức của vận tốc dựa trên tỉ lệ giảm tốc như sau:

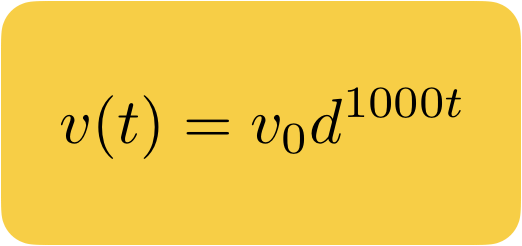
Ở đó:

? — vận tốc,
?ₒ — vận tốc ban đầu ở dạng pt/s (points per second),
d — deceleration rate (0 < d < 1),
t — thời gian.

Phương trình chuyển động

Không thể sử dụng chỉ mỗi hàm tính vận tốc để implement cơ chế giảm tốc. Vậy nên ta cần tìm phương trình chuyển động: sự phụ thuộc của toạ độ vào thời gian x(t). Và công thức vận tốc sẽ giúp chúng ta tìm ra phương trình chuyển động, chúng ta chỉ cần lấy nguyên hàm của phương trình vận tốc (tham khảo Ứng dụng nguyên hàm tích phân) và cuối cùng sẽ có:

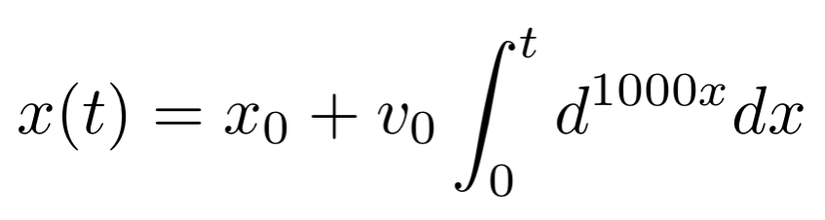
Sau đó thay thế công thức vận tốc cho v(x) và biến đổi, ta có:

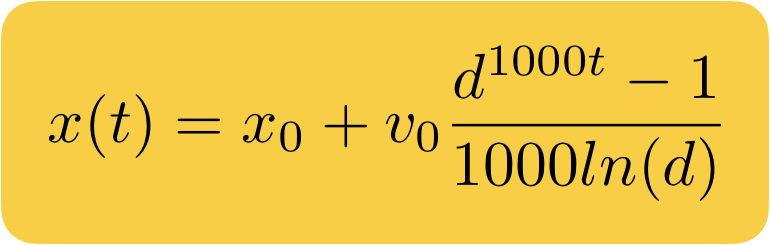
Phương trình điểm cuối

Now we can find the formula for the scroll endpoint, compare it with Apple’s formula, and test our reasoning. To do this, we need to direct time t to infinity. Since we have d less than one, and d¹⁰⁰⁰t converges to zero, we get:
VIETNAMESE
Bây giờ chúng ta có thể tìm công thức cho điểm cuối sau khi cuộn, so sánh nó với công thức của Apple và test xem. Để làm điều này, chúng ta cần hướng thời gian t đến vô cùng. Vì d < 1 và d¹⁰⁰⁰t hội tụ về 0, chúng ta sẽ có:

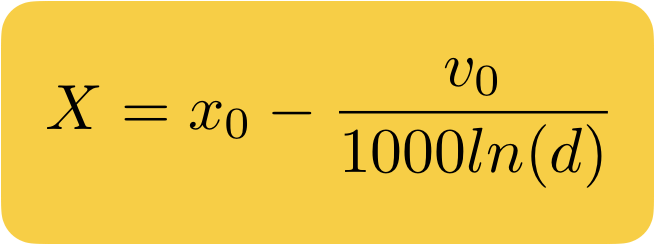
Giờ ta hãy thử so sánh công thức tìm được với công thức của Apple. Viết dưới cùng một dạng:

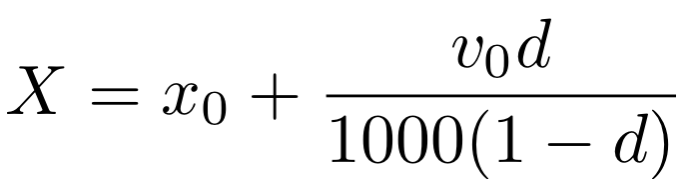
Và chúng ta dễ dàng nhận thấy rằng các công thức chỉ khác ở phần bên phải:

Tuy nhiên, nếu chúng ta nhìn vào cách logarit tự nhiên được phân tích thành một chuỗi Taylor trong vùng lân cận 1, chúng ta sẽ thấy rằng công thức Apple thực ra là một công thức gần đúng đối với công thức của chúng ta:

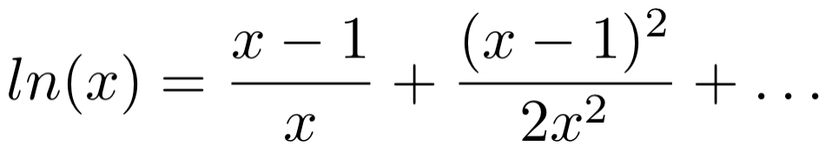
Về logarit tự nhiên: https://en.wikipedia.org/wiki/Naturallogarithm#Series

Nếu chúng ta vẽ đồ thị của các hàm này, chúng ta sẽ thấy rằng khi tiệm cận 1, chúng gần như trùng khớp:

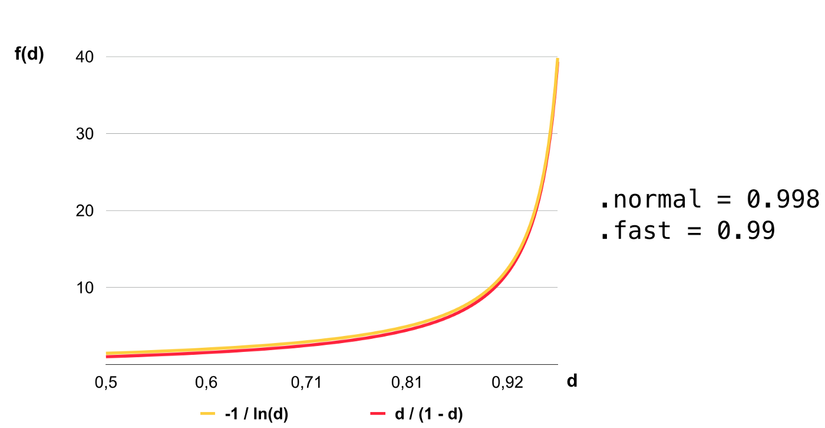
Các giá trị DecelerationRate mặc định rất gần với 1, do đó ta có thể thấy việc tối ưu của Apple khá là chuẩn. Việc tính logarit tốn performance hơn các phép toán thông thường kha khá.

Thời gian giảm tốc

Bây giờ việc còn lại của chúng ta chỉ là đi tìm thời gian giảm tốc để có thể implement animation. Để tìm điểm kết thúc, chúng ta đã hướng thời gian đến vô cùng. Nhưng để làm animation, thời gian sẽ phải là một con số giới hạn.

Nếu chúng ta vẽ phương trình chuyển động, chúng ta có thể thấy rằng hàm số đó khi tới vô cùng sẽ đến gần điểm cuối X. Tuy nhiên ở một thời điểm hữu hạn nhất định, hàm tiến tới điểm cuối X gần đến mức mà chuyển động không còn có thể nhìn thấy bằng mắt thường.

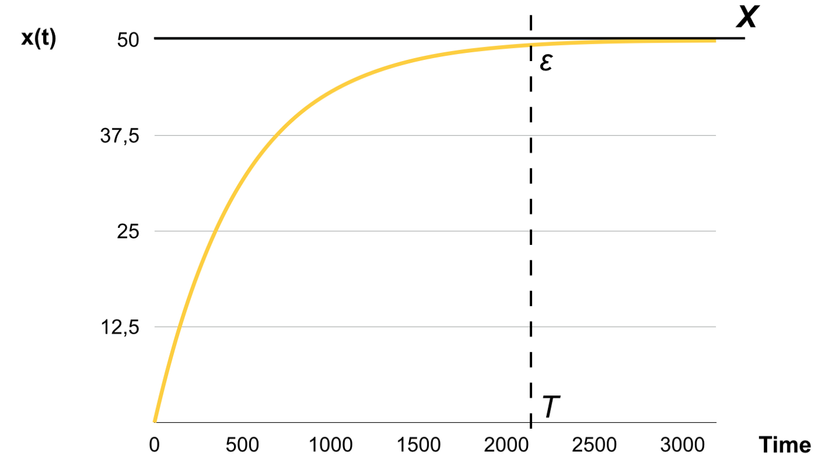
Do đó, chúng ta có thể định dạng lại bài toán của mình như sau: chúng ta tìm một khoảng thời gian T mà sau đó hàm tiến đủ gần điểm cuối X (bằng một khoảng cách nhỏ nào đó ε). Trong thực tế, ε có thể bằng với một nửa pixel, ví dụ vậy.

Hãy tìm T mà tại tại đó khoảng cách đến điểm cuối bằng ε:

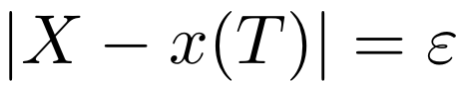
Thay thế công thức cho x và X và chúng ta sẽ nhận công thức cho thời gian chuyển động giảm tốc:

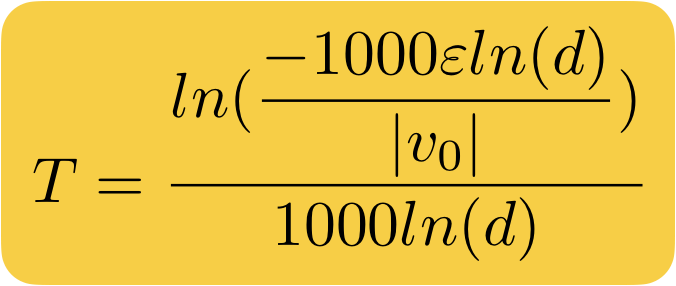
Và bây giờ chúng ta đã có toàn bộ thông tin cần thiết để tự implement cơ chế giảm tốc. Giờ hãy thử đưa một vài dòng code vào nhé!

Implement cơ chế giảm tốc

Để bắt đầu, hãy định nghĩa một struct DecelerationTimingParameters, struct này sẽ chứa tất cả thông tin cần thiết để tạo animation khi bạn bỏ ngón tay ra:

struct DecelerationTimingParameters {
    var initialValue: CGPoint
    var initialVelocity: CGPoint
    var decelerationRate: CGFloat
    var threshold: CGFloat
}

struct DecelerationTimingParameters {

var initialValue: CGPoint

var initialVelocity: CGPoint

var decelerationRate: CGFloat

var threshold: CGFloat

}

initialValue là contentOffset ban đầu – điểm mà chúng ta thả ngón tay ra
initialVelocity là vận tốc của gesture
decelerationRate là tỷ lệ giảm tốc
threshold là ngưỡng để tìm thời gian giảm tốc.

Sử dụng công thức, ta tìm được điểm dừng cuộn:

var destination: CGPoint {
    let dCoeff = 1000 * log(decelerationRate)
    return initialValue - initialVelocity / dCoeff
}

var destination: CGPoint {

let dCoeff = 1000 * log(decelerationRate)

return initialValue - initialVelocity / dCoeff

}

Thời gian giảm tốc:

var duration: TimeInterval {
    guard initialVelocity.length &gt; 0 else { return 0 }
    
    let dCoeff = 1000 * log(decelerationRate)
    return TimeInterval(log(-dCoeff * threshold / initialVelocity.length) / dCoeff)
}

var duration: TimeInterval {

guard initialVelocity.length > 0 else { return 0 }

let dCoeff = 1000 * log(decelerationRate)

return TimeInterval(log(-dCoeff * threshold / initialVelocity.length) / dCoeff)

}

Và phương trình chuyển động:

func value(at time: TimeInterval) -&gt; CGPoint {
    let dCoeff = 1000 * log(decelerationRate)
    return initialValue + (pow(decelerationRate, CGFloat(1000 * time)) - 1) / dCoeff * initialVelocity
}

func value(at time: TimeInterval) -> CGPoint {

let dCoeff = 1000 * log(decelerationRate)

return initialValue + (pow(decelerationRate, CGFloat(1000 * time)) - 1) / dCoeff * initialVelocity

}

We will use TimerAnimation, which will call the passed animation callback 60 times per second when the screen is updated (or 120 times per second on the iPad Pro), as the animation:
VIETNAMESE
Chúng ta sẽ sử dụng TimerAnimation, nó sẽ gọi animation callback mà ta truyền vào 60 lần mỗi giây khi màn hình được cập nhật (hoặc 120 lần mỗi giây trên iPad Pro):

class TimerAnimation {
    typealias Animations = (_ progress: Double, _ time: TimeInterval) -&gt; Void
    typealias Completion = (_ finished: Bool) -&gt; Void

    init(duration: TimeInterval, animations: @escaping Animations,
         completion: Completion? = nil)
}

class TimerAnimation {

typealias Animations = (_ progress: Double, _ time: TimeInterval) -> Void

typealias Completion = (_ finished: Bool) -> Void

init(duration: TimeInterval, animations: @escaping Animations,

completion: Completion? = nil)

}

Chúng ta sẽ tính toán contentOffset bằng phương trình chuyển động ở thời điểm hiện tại trong animation block để thay đổi cho phù hợp. TimerAnimation có thể được tìm thấy ở repo này.

Và giờ chúng ta sẽ cải thiện hàm xử lý gesture:

@objc func handlePanRecognizer(_ sender: UIPanGestureRecognizer) {
    switch sender.state {
    case .began:
        state = .dragging(initialOffset: contentOffset)
    case .changed:
        let translation = sender.translation(in: self)
        if case .dragging(let initialOffset) = state {
            contentOffset = clampOffset(initialOffset - translation)
        }
    case .ended:
        state = .default
    // Other cases
    }
}

@objc func handlePanRecognizer(_ sender: UIPanGestureRecognizer) {

switch sender.state {

case .began:

state = .dragging(initialOffset: contentOffset)

case .changed:

let translation = sender.translation(in: self)

if case .dragging(let initialOffset) = state {

contentOffset = clampOffset(initialOffset - translation)

}

case .ended:

state = .default

// Other cases

}

Quá trình giảm tốc sẽ bắt đầu khi ngón tay được thả ra. Do đó, khi trạng thái .end đến, chúng ta sẽ gọi hàm startDeceleration, truyền vận tốc của gesture cho nó:

@objc func handlePanRecognizer(_ sender: UIPanGestureRecognizer) {
    switch sender.state {
    case .began:
        state = .dragging(initialOffset: contentOffset)
    case .changed:
        let translation = sender.translation(in: self)
        if case .dragging(let initialOffset) = state {
            contentOffset = clampOffset(initialOffset - translation)
        }
    case .ended:
        state = .default
        let velocity = sender.velocity(in: self)
        startDeceleration(withVelocity: -velocity)

    // Other cases
    }
}

@objc func handlePanRecognizer(_ sender: UIPanGestureRecognizer) {

switch sender.state {

case .began:

state = .dragging(initialOffset: contentOffset)

case .changed:

let translation = sender.translation(in: self)

if case .dragging(let initialOffset) = state {

contentOffset = clampOffset(initialOffset - translation)

}

case .ended:

state = .default

let velocity = sender.velocity(in: self)

startDeceleration(withVelocity: -velocity)

// Other cases

}

Hàm startDeceleration sẽ được thực hiện như sau:

var contentOffsetAnimation: TimerAnimation?

func startDeceleration(withVelocity velocity: CGPoint) {
    let decelerationRate = UIScrollView.DecelerationRate.normal.rawValue
    let threshold = 0.5 / UIScreen.main.scale

    let parameters = DecelerationTimingParameters(initialValue: contentOffset, 
                                                  initialVelocity: velocity,
                                                  decelerationRate: decelerationRate, 
                                                  threshold: threshold)
    
    contentOffsetAnimation = TimerAnimation(
        duration: parameters.duration,
        animations: { [weak self] _, time in
            guard let self = self else { return }
            self.contentOffset = self.clampOffset(parameters.value(at: time))
        })
}

var contentOffsetAnimation: TimerAnimation?

func startDeceleration(withVelocity velocity: CGPoint) {

let decelerationRate = UIScrollView.DecelerationRate.normal.rawValue

let threshold = 0.5 / UIScreen.main.scale

let parameters = DecelerationTimingParameters(initialValue: contentOffset,

initialVelocity: velocity,

decelerationRate: decelerationRate,

threshold: threshold)

contentOffsetAnimation = TimerAnimation(

duration: parameters.duration,

animations: { [weak self] _, time in

guard let self = self else { return }

self.contentOffset = self.clampOffset(parameters.value(at: time))

})

}

Chọn DecelerationRate.normal và threshold tầm 1 nửa pixel.
Khởi tạo DecelerationTimingParameters.
Chạy animation, truyền animation time vào. Sau đó chúng ta sẽ gọi phương trình chuyển động trong animation block để cập nhật contentOffset.

Kết

Trên đây là các kiến thức liên quan đến cơ chế giảm tốc. Nếu nắm bắt được cơ chế này, chúng ta có thể dễ dàng custom và tạo ra những UI riêng rất mượt mà và tuân theo tiêu chuẩn về UX.
Chúc các bạn có một ngày làm việc vui vẻ.

Bài viết được dịch và tham khảo từ How UIScrollView works

Chia sẻ bài viết ngay

Nguồn bài viết : Viblo

[iOS] Tìm hiểu về cơ chế giảm tốc của UIScrollView

Hàm tính vận tốc (velocity function)

Phương trình chuyển động

Phương trình điểm cuối

Thời gian giảm tốc

Implement cơ chế giảm tốc

Kết

TikTok trở thành nền tảng mảng xã hội lớn thứ hai ở Nam Phi

Mất giá nhanh nhất sau 9 tháng ra mắt, iPhone 14 Pro Max tiếp tục phá đáy tại Việt Nam

Hướng dẫn sử dụng ngôn ngữ R cho người mới bắt đầu

10 plugin cần thiết của SublimeText dành cho các lập trình viên JavaScript