Understanding Preferred Search Tree (PST) Data Structure

Introduce

In computer science, priority search trees is a tree data structure for storing points in two-dimensional space (Oxy). The priority search tree was originally introduced by Edward McCreight in 1985 . The priority search tree is initially an extension of the priority queue with the aim of improving search time from: O ( n ) O (n) $O(n)$ comes O O $O$ S S $s$ l o g n log n $logn$

Figure 1: Example of a preferred search tree:

How to build a PST tree

The preferred lookup tree is a data structure that stores points in a 2-dimensional space. First, we consider n points on the same plane, each with the x and y coordinates shown in Figure 2. The problem of constructing the preferred search tree is described as follows: Input : We have n points in the plane S S $S$ = { p i p_ {i} p i │ $i$ $=$ $first$ $,$ $2$ $,$ $3$ $\dots$ $n$ $i\; =\; 1,2,3\dots \; n$ i = 1 , 2 , 3 … n } and points $p$$i$ $($ $p$$i$$.$$x$ $,$ $p$$i$$.$$y$ $)$ $p\_i\; (p\_i.x,\; p\_i.y)$ p i (P i . x, p i . y ) . Output: The search tree prioritizes to store points in 2-dimensional space.

Sequence:

1. If S = NULL, NULL is returned.
2. Find the point p i p_ {i} p i has the smallest y-coordinate set as root, $p$ $i$ $p\_\; \{i\}$ p i = min ⁡ $p$ $i$ $p\_\; \{i\}$ p i .y ∊S}
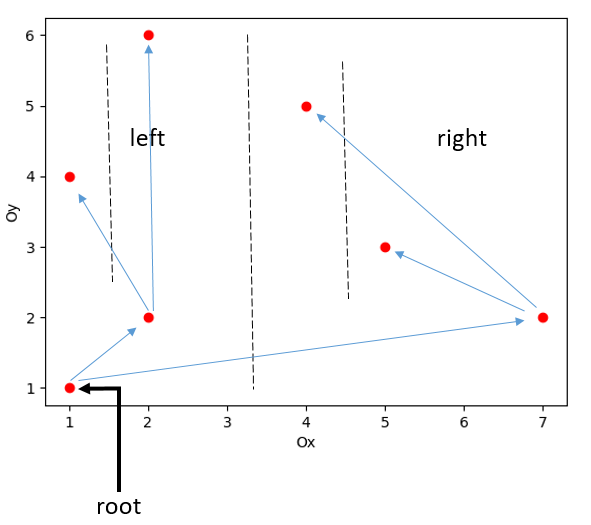
3. Find the median dividing points to the left and right. On the left side look for points p i p_ {i} p i = min { $p$ $i$ $p\_\; \{i\}$ p i .y ∊ $S$ $l$ $S\_l$ S l { $p$ $p$ $a$ $r$ $e$ $n$ $t$ $p\_\; \{parent\}$ p r e p a n t }} assign as the child of the parent node in step 2 , do the same with the right side shown in Figure 3 .
4. Recursively recursive PST (s) with the left side.
5. Recursively recursive PST (s) with right side.
6. End.

Figure 2: Representation of points on the oxygen plane

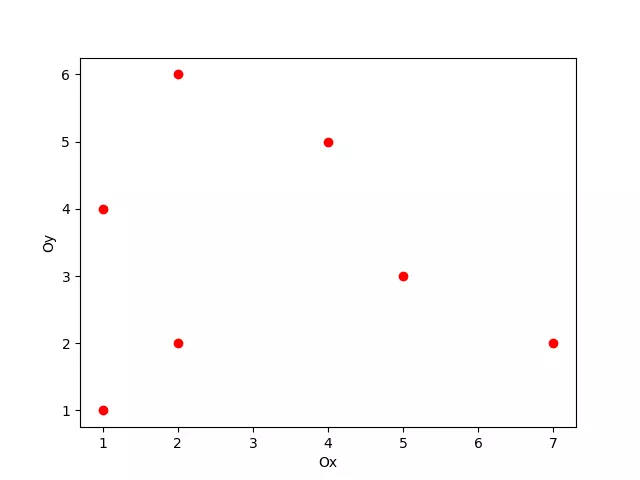
Figure 3: Description of PST tree construction

Decoding code is written in pascal:

Add a new node to the tree

Next comes the problem of adding a new node to the tree. Suppose there is a new node with coordinates x n e w x_ {new} x n e w and $y$ $n$ $e$ $w$ $y\_\; \{new\}$ y n e w need to be added to the tree. Thus, we will need to recalculate if there is a change in the root and the medians. It then compares whether the new node can be inserted in the stump or the nodes on the left and right sides.

The pascal decoder adds a new node to the tree:

Delete the node from the tree

Next comes the problem of adding a new node to the tree. Suppose there is an old node with coordinates x o l d x_ {old} x o l d and $y$ $o$ $l$ $d$ $y\_\; \{old\}$ y o l d need to be removed from the tree. Thus, we need to recalculate if there is a change in the stump, the parent nodes, the medians and update the tree again.

The pascal decoder removes a node from the tree:

Query points in the tree

Next, let’s look at tree search. The preferred search tree can help find points that satisfy conditions on the oxygen plane, which is different from a binary search tree (BST) that searches only 1 point in the tree. When searching, we need to define the search scope in the form of limited rectangles x m i n x_ {min} x m i n and $x$ $m$ $a$ $x$ $x\_\; \{max\}$ x m a x and priority y. In the figure below consider the problem of finding points on the search tree with priority $y$ $m$ $a$ $x$ $y\_\; \{max\}$ y m a x as original.

Figure 4: Description of the search scope

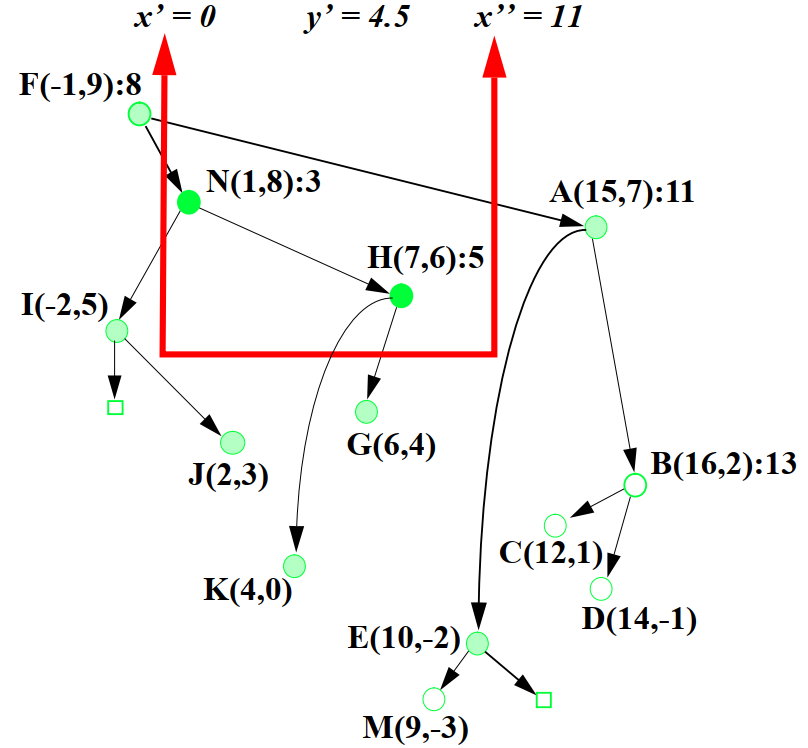
Figure 5: Description of search method

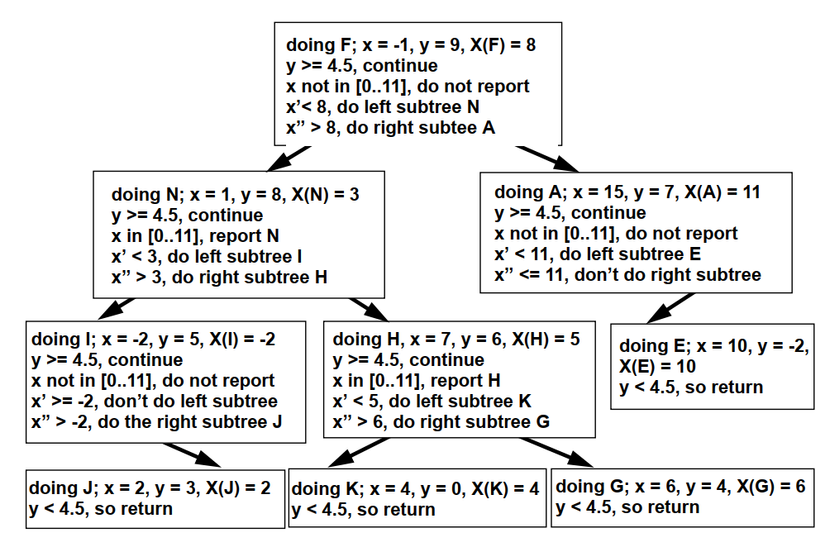
Decode the search algorithm pascal:

Implementation algorithm with Python:

The problem of finding the point with the smallest y

The problem is finding a point with the smallest y-coordinate in a given rectangular range on the oxygen plane. With the naked eye, we can immediately see the desired point in the range with the small number of points in the plane. If you find sequentially comparing each point with each other, the complexity of the algorithm will be O ( n ) O (n) $O(n)$ . Therefore, we use a preferred search tree data structure to perform searches with word complexity O ( n ) O (n) $O(n)$ O O $O$ S S $s$lognlog n$logn$

Algorithm code:

The problem of finding the point with the largest x

The problem is finding a point with the largest x coordinate in a given rectangular range on the oxygen plane. With the naked eye, we can immediately see the desired point in the range with the small number of points in the plane. If you find sequentially comparing each point with each other, the complexity of the algorithm will be O ( n ) O (n) $O(n)$ . Therefore, we use a preferred search tree data structure to perform searches with word complexity O ( n ) O (n) $O(n)$ O O $O$ S S $s$lognlog n$logn$

Algorithm code:

Download the source code

See the entire source code in python at github

Refer

[1] McCreight, Edward (May 1985). “Priority search trees”. SIAM Journal on Scientific Computing.

[2] DT Lee. “Interval, Range, and Priority Search Tree”. Academia Sinica.

[3] Dina Q Goldin Karon (March 8, 1993). “Priority Search Tree”. Computational Geometry.