Introduction to Cryptosystem on an Elliptic Curve (ECC)

Tram Ho

Elliptic curves are widely used in cryptography and information technology. I must confess that when I first learned about the concept of Cryptography on an Elliptic Curve (Elliptic Curve Cryptography, or ECC for short) I did not understand at all: “What is this so high?” This happened four months ago, when I read this article.

But when we learn more about ECC, we find this an interesting and interesting “curve”, so let’s find out. Rest assured, I will try to explain in the easiest way to understand so that you do not have to say like me before: “What’s this sublime thing?”

1. Mathematical basis 1000%

The number of mathematical theories needed to understand to be able to explain this magical curve is so much. As in a document I have read, Mr. Tuan Vietkey has listed “some” theories as follows:

  • Group theory, ring, field in abstract algebra
  • Affine manifolds, Jacobian manifolds, and photographic manifolds in algebraic geometry
  • Torsion point, Divisor, Weil parallel pair, Tate-Lichtenbaum
  • Galois field theory, Frobenius self-isomorphic-mappings
  • The Baker-Feldman, Baker-Tijdeman theory and Kummer theory
  • The p-adic number, Isogenies function, the Sigma function and the Zeta function
  • Group of homosexuality, Galois homosexuality and non-commutative homogeneity
  • The Mordell – Weil, Selmer and Shafarevich – Tate groups
  • Method of geometry and linear title (Quasilinear)

With such theories, I have to bear, but basically, the Elliptic curve has the general form of the Weierstrass equation as follows:

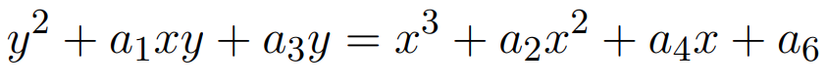
After a number of substitutions and transformations, the reduced equation only leaves:

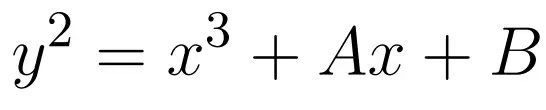
With the conditions:

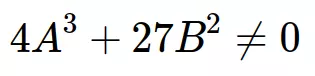
And this is also the main form that appears in documents.

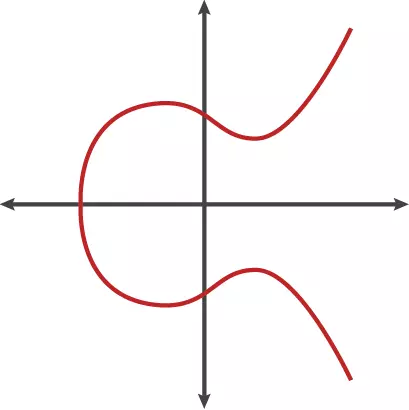
Usually the graph of an elliptic curve is represented as follows:

However, this is just a cross section, in 3D space the Elliptic curve looks like this:

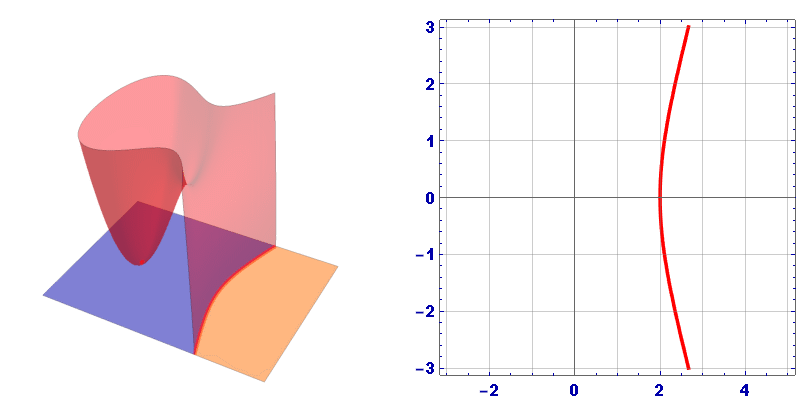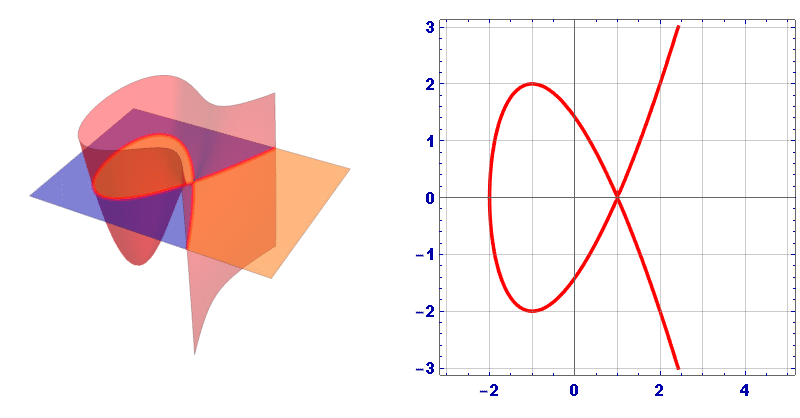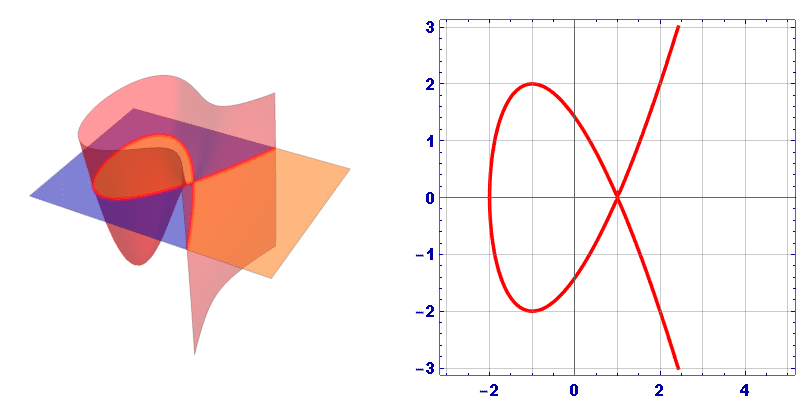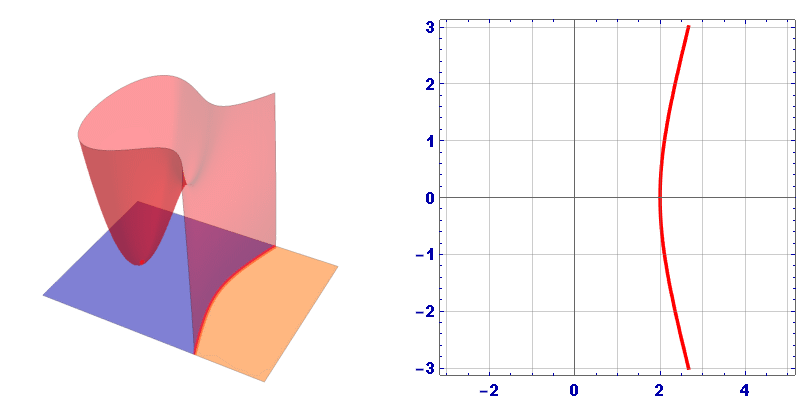
1.1. Addition on an Elliptic Curve

Addition on this curve is real virtual !!!

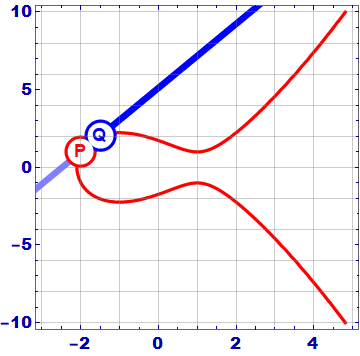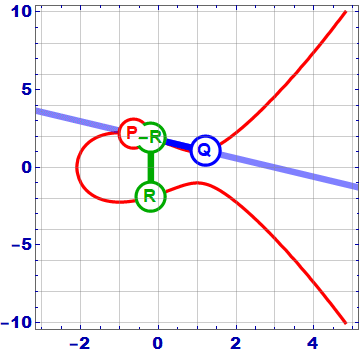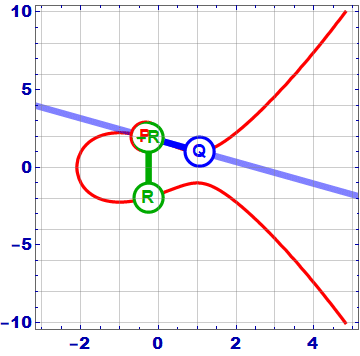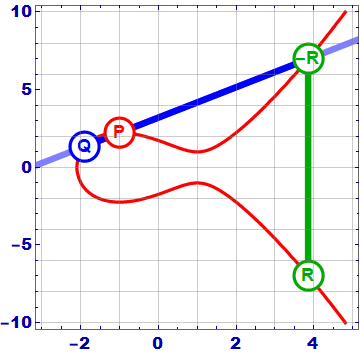
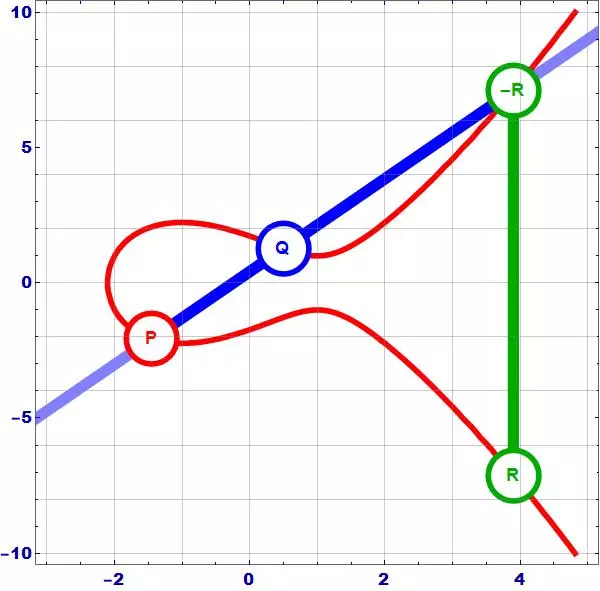
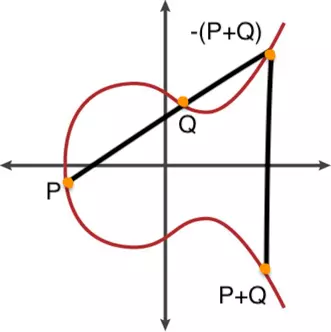
As the gif shows, the addition of 2 points P and Q on an elliptic curve works as follows:

  • Draw the line A through 2 points P and Q.
  • Line A intersects the Elliptic curve at -R = – (P + Q)
  • Get the symmetry point across the axis Ox, we get the point R = (P + Q)

In the case where the points P and Q coincide , the line A is tangent to the curve at point P. Do the same to get 2P score.

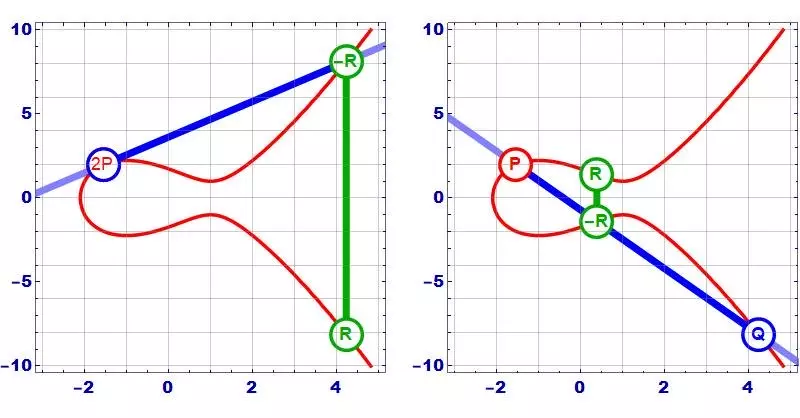
1.2. Multiplication on an Elliptic Curve

Once we understand addition, we can easily understand how multiplication on an elliptic curve works. Because multiplication is essentially doing addition many times. Perform the 3P multiplication, first we calculate 2P = P + P, then calculate 3P = 2P + P.

Calculation of nP can be done according to the Multiplication and addition method . First, represent the number n as:

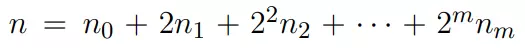
With the conditions:

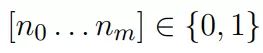
Then apply the algorithm:

Note

On the Elliptic Curve does not exist :

  • Multiplication of 2 points P x Q on an elliptic curve
  • Scalar division Q: n (where Q = nP)
    Finding n is the discrete Logarithmic problem – a problem that is difficult to solve in polynomial time.

2. ECC is widely used in cryptography

2.1. High security

ECC belongs to public key encryption, which means there will be 2 different keys for 2 decryption – encryption processes. Since everyone can access the public key, the secret system must have a high degree of computational difficulty to prevent finding the private key from the public key. The security of ECC is based on the complexity of the discrete Logarithmic problem on an Elliptic Curve. Currently, there is no algorithm capable of calculating with times less than exponentiation.

Since there is no division on an elliptic curve, for Q = nP , when giving us a point Q and a starting point P, the way to find n is usually to try n = 1, 2, … n-1 until you find the result nP = Q. Basically, it is impossible to compute n in polynomial time.

I will talk about the discrete Logarithmic problem later. However, to make it easier to visualize, we can think like this: By addition on an elliptic curve

2.2. Save on computation costs

Factors to consider for each cryptosystem are:

  • Price
  • Efficiency
  • Safety

Of course, customers (users) always want to use the best technology, but the cost (or price) must be as low as possible. So a good, widely used cryptosystem must balance the above three criteria well (Note that the cost here is the amount of hardware resources, the computational cost required for encryption and decryption). .

ECC did a good job of this. As I mentioned above, ECC belongs to public key encryption, however when it comes to public encryption people often think of RSA first. RSA is a good public key encryption algorithm, can be applied in digital signature authentication, … However, the security of RSA is based on the problem of analyzing large integers to prime factors. This also creates a big problem: if we want to ensure the security of the cryptosystem, we will need to choose two large primes, at least about 2048 bits or according to the PCI standard, the key length should be 4096. bit.

4096 bits is a very large number, even 2048 bits are large. This makes calculating with these large integers difficult and consuming a lot of hardware resources, computation time, … Not to mention that if the algorithm is not good, it can lead to incorrect calculation with data. is too long. ECC has greatly reduced computation costs, while still ensuring the security of the cryptosystem.

Some figures comparing ECC and RSA:

ECCRSA
256 bit key3072 bit key
384 bit key7680 bit key

The 384-bit ECC rated by the NSA is sufficient to protect the information at TOP SECRET level.

Part 1 of the series on Cryptosystems on Elliptic Curves ends here. In the next section, I will talk about Elliptic Curve Ciphers.

References:

Share the news now

Source : Viblo