ECDSA – cryptographic system based on Elliptic curve and application in Blockchain

Wednesday, 13/05/2020

Tram Ho

Intro

ECDSA stands for Elliptic Curve Digital Signature Algorithm – the digital signature generation algorithm based on Elliptic curves.

ECDSA is used to create digital signatures for data, helps prevent tampering and falsify data, providing an authentication method without compromising the security of the original data.

ECDSA is widely used in many fields that need data security and privacy, especially in Blockchain .

In this article I will present an overview of ECDSA in general and its application in Blockchain in particular.

Why use ECDSA?

ECDSA is an asymmetric encryption algorithm.

It differs from other symmetric ciphers such as AES, we have a unique key to encrypt data and decode. It means knowing the key is knowing everything, and not knowing the key knows nothing.

ECDSA is different, it has a pair of private key and public key . private key for encryption, the public key for verifying the correctness of this encrypted data, and that’s it. public key cannot decrypt encrypted data, so the original data is always safe.

Why use asymmetric encryption? Its usefulness is shown in its ability to create digital signatures . For each document, transaction, or any data, we can create a data with signature . This signature can only be created by someone who has information about the secret key, and anyone can access the public key to be able to verify this signature. This useful attribute of asymmetric cryptography allows anyone to verify every signature on every transaction, while ensuring that only secret key owners can create the word. signed valid.

Secret key and public key

Secret key

A private key is merely a randomly chosen number.

As the name implies, the private key needs to be kept secret, so choosing a random number must be extremely secure and really random to avoid emptying attacks or other attacks. Get the private key .

Why is the private key important? because it creates a signature , and proves that the data, or property belongs to the owner of the private key.

Therefore, protecting the private key is extremely important. Absolutely do not share the private key with anyone else, and keep the private key in a safe place, because once lost will not be restored, meaning that we may lose all authentication rights. with our data or property.

Public key

Unlike the private key , the public key is public for everyone.

public key is created by multiplying with the private key in the Elliptic curve , we will talk more about in the next section.

Elliptic curve multiplication is a trap door operation , meaning it is easy to calculate in one direction (multiplication) and cannot be calculated in the opposite direction (division).

Therefore, the owner of the private key can easily create a public key and share with people without worrying that someone can reverse the public key to take over his private key .

This theory forms the basis for secure and impersonal digital signatures, for example used to prove ownership of Bitcoin or Ethereum on blockchain networks.

Elliptic curve

Recipe

The formula for the Elliptic curve is:

$y^{2} (m o d p) = x^{3} + a x + b (m o d p)$

Bitcoin or Ethereum use a curve according to the secp256k1 standard set by the National Institute of Standards and Technology (NIST).

This curve has the following formula:

$y^{2} (m o d p) = x^{3} + 7 (m o d p)$

where p is a very large prime number, $p = 2 ^ {265} – 2 ^ {32} – 2 ^ 9 – 2 ^ 8 – 2 ^ 7 – 2 ^ 6 – 2 ^ 4 – 1$ $p = 2^{265} - 2^{32} - 2^{9} - 2^{8} - 2^{7} - 2^{6} - 2^{4} - 1$ .

The figure below illustrates the elliptic curve used in Bitcoin & Ethereum.

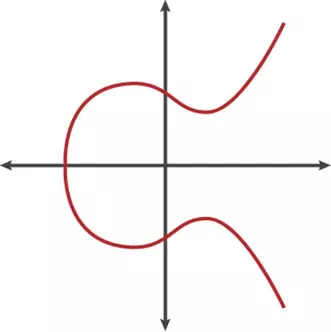
Operations on Elliptic curves

There are two important operations on an elliptic curve: addition and multiplication

Summation

The Elliptic curve has a property: “If both P and Q are on the curve, then P + Q will be on the curve”.

This point is determined as follows:

Draw a line connecting two points P and Q, this line will cut the curve at another point
Taking the symmetry of this point across the horizontal axis, we get P + Q

The figure below illustrates how addition is performed in an Elliptic curve:

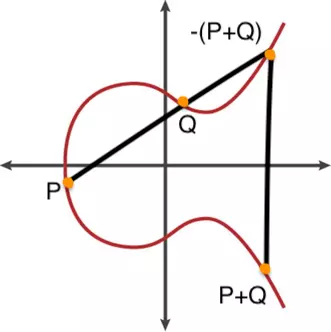
If the 3 points on the Elliptic curve are straight, then their sum is 0.

Multiplication

On the Elliptic curve, multiplying a point by a constant is not simply taking each coordinate and then multiplying.

Actually, multiplication here is still addition , but done many times only.

For example in the 3P calculation, we will first calculate 2P by calculating P+P

In the addition way above, we draw a line connecting P and P, here is the tangent of the curve, it intersects the curve at point -2P , symmetrically across the horizontal axis we have 2P .

Continue drawing a line connecting 2P and P , cutting the curve at -3P , taking the symmetry we have 3P .

The figure below illustrates how multiplication is performed in an elliptic curve:

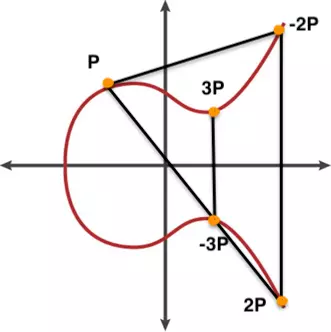
Because of the above calculation, it is easy to calculate the multiplication k*P when knowing k and P , but it is absolutely impossible to calculate the opposite direction, ie division. That is also the interesting characteristic of asymmetric encryption.

Generate public key

We have a private key is a random number $d_{A}$ .

On the Elliptic curve we choose a G point, called a generator point or reference point.

Public key $Q_A$ $Q_{A}$ was born as a result of multiplication:

$Q_A = d_A times G$ $Q_{A} = d_{A} \times G$

With Bitcoin or Ethereum:

<span class="token constant">G</span> <span class="token operator">=</span> <span class="token number">04</span> <span class="token number">79</span> BE667E <span class="token constant">F9DCBBAC</span> <span class="token number">55</span> A06295 <span class="token constant">CE870B07</span> <span class="token number">029</span> BFCDB <span class="token number">2</span> DCE28D9 <span class="token number">59</span> F2815B <span class="token number">16</span> F81798 <span class="token number">483</span> ADA77 <span class="token number">26</span> A3C465 <span class="token number">5</span> DA4FBFC <span class="token number">0E1108</span> A8 <span class="token constant">FD17B448</span> <span class="token constant">A6855419</span> <span class="token number">9</span> C47D08F <span class="token constant">FB10D4B8</span>

G = 04 79 BE667E F9DCBBAC 55 A06295 CE870B07 029 BFCDB 2 DCE28D9 59 F2815B 16 F81798 483 ADA77 26 A3C465 5 DA4FBFC 0E1108 A8 FD17B448 A6855419 9 C47D08F FB10D4B8

according to secp256k1 standard.

Of course $Q_A$ $Q_{A}$ will also be a point on the elliptic curve.

Relationship between $d_{A}$ and $Q_A$ $Q_{A} is fixed, and computes only in one direction$ $d_{A} come$ $Q_A$ $Q_{A} . That is why we can generate the public key from the secret key and we can share this public key with everyone, but we cannot use the public key to find the reverse key to the secret key.$

ECDSA – Digital signature based on Elliptic curve

We have learned the theory of elliptic curves, private keys, public keys, in this section we will learn how a file / message is signed in Ethereum and how it creates digital signatures.

Create signature

The signature in Ethereum will be represented by a pair (r, s) .

To create this (r, s) pair (r, s) first we will have to pick a random number k (note this is a random number different from the private key).

Then multiply k by the birth point G like the math we used to create the above pubic key:

$P = k \times G$

then we have a point P(x, y) , the x coordinate of P is the value of r .

To calculate s , we first calculate the hash of the message we need to sign, called z (in Ethereum, the hash function is Keccak256 ), then:

$d_A times r) pmod p$ $s = k^{- 1} (z + d_{A} \times r) (m o d p)$

I note here $k ^ {- 1}$ $k^{- 1}$ is the inverse modulo of k , see more ( modular multiplicative inverse ) rather than the simple inverse in decimal calculations is $k 1 .$

If in the decimal calculation $k times frac {1} {k} = 1$ $k \times k 1 = 1$ is modulo $k \times k ^{- 1} \equiv first ( m o d m ) .$

The inverse example of 2 in decimal calculations is $frac {1} {2}$ $2 1$ because $2 \times 2 1 = 1 . But the inverse modulo 5 of 2 would be 3 because$ $2 \times 3 = 6 \equiv first ( m o d 5 ) . So$ $2 ^{- 1} = 3 (m o d 5) .$

Verify signature

To verify the validity of the signature, we only need the public key $Q_A$ $Q_{A}$ is enough.

By calculation:

$Q_A$ $P = s^{- 1} \times z \times G + s^{- 1} \times r \times Q_{A}$

If the x coordinate of P equals r , that means the signature is valid.

We will prove this as follows:

$Q_A$ $P = s^{- 1} \times z \times G + s^{- 1} \times r \times Q_{A}$

but $Q_A = d_A times G$ $Q_{A} = d_{A} \times G$

Candlestick $d_A) times s ^ {- 1} times G$ $P = (z + r \times d_{A}) \times s^{- 1} \times G$

that we have $d_A times r)$ $s = k^{- 1} (z + d_{A} \times r)$

infer $d_A) times (z + r times d_A) ^ {- 1} times (k ^ {- 1}) ^ {- 1} times G$ $P = (z + r \times d_{A}) \times (z + r \times d_{A})^{- 1} \times (k^{- 1})^{- 1} \times G$

$\Leftrightarrow P = k \times G$

This is the formula we use to calculate P when creating a signature, so we have something to prove.

Application in Ethereum

In Ethereum (Bitcoin is similar), the Elliptic curve is applied in two things:

Create wallet address
Create a signature for the transaction

In this section we will use code to reduce the complexity of the calculation.

Create wallet address

From a private key, an Ethereum wallet address is created as follows

Create the public key from the private key as we have shown above.
Calculate the public key’s hash and take the last 20 bytes as the address, the hash function here is Keccak256

For example, we have a private key:

dA <span class="token operator">=</span> f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

1 2	dA <span class="token operator">=</span> f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

by multiplying Elliptic curves, we calculate the public key as a point $Q_A = (x, y)$ $Q_{A} = (x, y)$ with

x <span class="token operator">=</span> <span class="token number">6e145</span> ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b
y <span class="token operator">=</span> <span class="token number">83</span> b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

x = 6e145 ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b

y = 83 b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

Paired into it, we will have a public key

<span class="token constant">QA</span> <span class="token operator">=</span> <span class="token number">0x6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0</span>

1 2	<span class="token constant">QA</span> <span class="token operator">=</span> <span class="token number">0x6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0</span>

Conducting a hash of public key, we can

<span class="token function">Keccak256</span> <span class="token punctuation">(</span> <span class="token constant">QA</span> <span class="token punctuation">)</span> <span class="token operator">=</span> <span class="token number">2</span> a5bc342ed616b5ba5732269001d3f1ef827552ae1114027bd3ecf1f086ba0f9

Keccak256 ( QA ) = 2 a5bc342ed616b5ba5732269001d3f1ef827552ae1114027bd3ecf1f086ba0f9

Get the last 20 bytes we will get the main wallet address is 0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

Code:

<span class="token keyword">var</span> Wallet <span class="token operator">=</span> <span class="token function">require</span> <span class="token punctuation">(</span> <span class="token string">'ethereumjs-wallet'</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>
<span class="token keyword">var</span> EthUtil <span class="token operator">=</span> <span class="token function">require</span> <span class="token punctuation">(</span> <span class="token string">'ethereumjs-util'</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>

<span class="token keyword">const</span> privateKeyBuffer <span class="token operator">=</span> EthUtil <span class="token punctuation">.</span> <span class="token function">toBuffer</span> <span class="token punctuation">(</span>
  <span class="token string">'0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315'</span>
<span class="token punctuation">)</span> <span class="token punctuation">;</span>
<span class="token keyword">const</span> wallet <span class="token operator">=</span> Wallet <span class="token punctuation">.</span> <span class="token function">fromPrivateKey</span> <span class="token punctuation">(</span> privateKeyBuffer <span class="token punctuation">)</span> <span class="token punctuation">;</span>

<span class="token keyword">const</span> publicKey <span class="token operator">=</span> wallet <span class="token punctuation">.</span> <span class="token function">getPublicKeyString</span> <span class="token punctuation">(</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>
console <span class="token punctuation">.</span> <span class="token function">log</span> <span class="token punctuation">(</span> <span class="token punctuation">{</span> publicKey <span class="token punctuation">}</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>
<span class="token keyword">const</span> address <span class="token operator">=</span> wallet <span class="token punctuation">.</span> <span class="token function">getAddressString</span> <span class="token punctuation">(</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>
console <span class="token punctuation">.</span> <span class="token function">log</span> <span class="token punctuation">(</span> <span class="token punctuation">{</span> address <span class="token punctuation">}</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>

var Wallet = require ( 'ethereumjs-wallet' ) ;

var EthUtil = require ( 'ethereumjs-util' ) ;

const privateKeyBuffer = EthUtil . toBuffer (

'0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315'

) ;

const wallet = Wallet . fromPrivateKey ( privateKeyBuffer ) ;

const publicKey = wallet . getPublicKeyString ( ) ;

console . log ( { publicKey } ) ;

const address = wallet . getAddressString ( ) ;

console . log ( { address } ) ;

Sign the transaction

A raw transaction in Ethereum would look like this:

<span class="token punctuation">{</span>
  <span class="token keyword">from</span> <span class="token punctuation">:</span> <span class="token string">'0x937CDc3a7273269Fe43967E785D9e24D3C48C164'</span> <span class="token punctuation">,</span>
  gas <span class="token punctuation">:</span> <span class="token string">'0x3d0900'</span> <span class="token punctuation">,</span>
  gasPrice <span class="token punctuation">:</span> <span class="token number">10000000000</span> <span class="token punctuation">,</span>
  hash <span class="token punctuation">:</span> <span class="token string">'0x228c53215e5ad0f9d6114a4f4adeb8e5359fbee1283aacb7fedb2ab1b212871b'</span> <span class="token punctuation">,</span>
  data <span class="token punctuation">:</span> <span class="token string">'0x60fe47b10000000000000000000000000000000000000000000000000000000000000003'</span> <span class="token punctuation">,</span>
  nonce <span class="token punctuation">:</span> <span class="token number">34</span> <span class="token punctuation">,</span>
  to <span class="token punctuation">:</span> <span class="token string">'0x6b4A7a46ad065b5fb142DEe92E9F4546982510fD'</span> <span class="token punctuation">,</span>
  value <span class="token punctuation">:</span> <span class="token string">'0x'</span> <span class="token punctuation">,</span>
<span class="token punctuation">}</span>

{

from : '0x937CDc3a7273269Fe43967E785D9e24D3C48C164' ,

gas : '0x3d0900' ,

gasPrice : 10000000000 ,

hash : '0x228c53215e5ad0f9d6114a4f4adeb8e5359fbee1283aacb7fedb2ab1b212871b' ,

data : '0x60fe47b10000000000000000000000000000000000000000000000000000000000000003' ,

nonce : 34 ,

to : '0x6b4A7a46ad065b5fb142DEe92E9F4546982510fD' ,

value : '0x' ,

}

We will proceed with the signing of the private key as follows:

<span class="token keyword">let</span> tx <span class="token operator">=</span> <span class="token keyword">new</span> <span class="token class-name">EthereumTx</span> <span class="token punctuation">(</span> rawTx <span class="token punctuation">)</span> <span class="token punctuation">;</span>
console <span class="token punctuation">.</span> <span class="token function">log</span> <span class="token punctuation">(</span> <span class="token string">'mess: '</span> <span class="token punctuation">,</span> tx <span class="token punctuation">.</span> <span class="token function">hash</span> <span class="token punctuation">(</span> <span class="token boolean">false</span> <span class="token punctuation">)</span> <span class="token punctuation">.</span> <span class="token function">toString</span> <span class="token punctuation">(</span> <span class="token string">'hex'</span> <span class="token punctuation">)</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>
tx <span class="token punctuation">.</span> <span class="token function">sign</span> <span class="token punctuation">(</span> privateKey <span class="token punctuation">)</span> <span class="token punctuation">;</span>
<span class="token keyword">let</span> serializedTx <span class="token operator">=</span> tx <span class="token punctuation">.</span> <span class="token function">serialize</span> <span class="token punctuation">(</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>
<span class="token keyword">await</span> web3 <span class="token punctuation">.</span> eth
  <span class="token punctuation">.</span> <span class="token function">sendSignedTransaction</span> <span class="token punctuation">(</span> <span class="token string">'0x'</span> <span class="token operator">+</span> serializedTx <span class="token punctuation">.</span> <span class="token function">toString</span> <span class="token punctuation">(</span> <span class="token string">'hex'</span> <span class="token punctuation">)</span> <span class="token punctuation">)</span>
  <span class="token punctuation">.</span> <span class="token function">on</span> <span class="token punctuation">(</span> <span class="token string">'transactionHash'</span> <span class="token punctuation">,</span> <span class="token punctuation">(</span> hash <span class="token punctuation">)</span> <span class="token operator">=&gt;</span> <span class="token punctuation">{</span>
    console <span class="token punctuation">.</span> <span class="token function">log</span> <span class="token punctuation">(</span> <span class="token string">'tx hash: '</span> <span class="token punctuation">,</span> hash <span class="token punctuation">)</span> <span class="token punctuation">;</span>
  <span class="token punctuation">}</span> <span class="token punctuation">)</span>
  <span class="token punctuation">.</span> <span class="token function">on</span> <span class="token punctuation">(</span> <span class="token string">'receipt'</span> <span class="token punctuation">,</span> <span class="token punctuation">(</span> receipt <span class="token punctuation">)</span> <span class="token operator">=&gt;</span> <span class="token punctuation">{</span>
    console <span class="token punctuation">.</span> <span class="token function">log</span> <span class="token punctuation">(</span> <span class="token string">'tx successfull'</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>
  <span class="token punctuation">}</span> <span class="token punctuation">)</span>
  <span class="token punctuation">.</span> <span class="token function">on</span> <span class="token punctuation">(</span> <span class="token string">'error'</span> <span class="token punctuation">,</span> <span class="token punctuation">(</span> err <span class="token punctuation">)</span> <span class="token operator">=&gt;</span> <span class="token punctuation">{</span>
    console <span class="token punctuation">.</span> <span class="token function">log</span> <span class="token punctuation">(</span> <span class="token string">'wrong '</span> <span class="token punctuation">,</span> err <span class="token punctuation">)</span> <span class="token punctuation">;</span>
  <span class="token punctuation">}</span> <span class="token punctuation">)</span> <span class="token punctuation">;</span>

let tx = new EthereumTx ( rawTx ) ;

console . log ( 'mess: ' , tx . hash ( false ) . toString ( 'hex' ) ) ;

tx . sign ( privateKey ) ;

let serializedTx = tx . serialize ( ) ;

await web3 . eth

. sendSignedTransaction ( '0x' + serializedTx . toString ( 'hex' ) )

. on ( 'transactionHash' , ( hash ) => {

console . log ( 'tx hash: ' , hash ) ;

} )

. on ( 'receipt' , ( receipt ) => {

console . log ( 'tx successfull' ) ;

} )

. on ( 'error' , ( err ) => {

console . log ( 'wrong ' , err ) ;

} ) ;

Then we will have a signed transaction and ready to broadcast on the network then:

<span class="token punctuation">{</span>
  blockHash <span class="token punctuation">:</span> <span class="token string">'0x7905dc70c9a0196fd2a1999568506026e5e4027c7fac88fd3b841df213c7918d'</span> <span class="token punctuation">,</span>
  blockNumber <span class="token punctuation">:</span> <span class="token number">7719658</span> <span class="token punctuation">,</span>
  <span class="token keyword">from</span> <span class="token punctuation">:</span> <span class="token string">'0x937CDc3a7273269Fe43967E785D9e24D3C48C164'</span> <span class="token punctuation">,</span>
  gas <span class="token punctuation">:</span> <span class="token string">'0x3d0900'</span> <span class="token punctuation">,</span>
  gasPrice <span class="token punctuation">:</span> <span class="token string">'10000000000'</span> <span class="token punctuation">,</span>
  hash <span class="token punctuation">:</span> <span class="token string">'0x228c53215e5ad0f9d6114a4f4adeb8e5359fbee1283aacb7fedb2ab1b212871b'</span> <span class="token punctuation">,</span>
  input <span class="token punctuation">:</span> <span class="token string">'0x60fe47b10000000000000000000000000000000000000000000000000000000000000003'</span> <span class="token punctuation">,</span>
  nonce <span class="token punctuation">:</span> <span class="token number">34</span> <span class="token punctuation">,</span>
  r <span class="token punctuation">:</span> <span class="token string">'0x3dee14909e26ec8758cca4b386ec582cac5100767776454eec94343ac6f2de46'</span> <span class="token punctuation">,</span>
  s <span class="token punctuation">:</span> <span class="token string">'0x68869c7b5e4b4caa6b602e29f0787ae70a37833cc681c9463b139f30a2fe5de5'</span> <span class="token punctuation">,</span>
  to <span class="token punctuation">:</span> <span class="token string">'0x6b4A7a46ad065b5fb142DEe92E9F4546982510fD'</span> <span class="token punctuation">,</span>
  transactionIndex <span class="token punctuation">:</span> <span class="token number">2</span> <span class="token punctuation">,</span>
  v <span class="token punctuation">:</span> <span class="token string">'0x29'</span> <span class="token punctuation">,</span>
  value <span class="token punctuation">:</span> <span class="token string">'0'</span> <span class="token punctuation">,</span>
<span class="token punctuation">}</span> <span class="token punctuation">;</span>

{

blockHash : '0x7905dc70c9a0196fd2a1999568506026e5e4027c7fac88fd3b841df213c7918d' ,

blockNumber : 7719658 ,

gas : '0x3d0900' ,

gasPrice : '10000000000' ,

hash : '0x228c53215e5ad0f9d6114a4f4adeb8e5359fbee1283aacb7fedb2ab1b212871b' ,

input : '0x60fe47b10000000000000000000000000000000000000000000000000000000000000003' ,

nonce : 34 ,

r : '0x3dee14909e26ec8758cca4b386ec582cac5100767776454eec94343ac6f2de46' ,

s : '0x68869c7b5e4b4caa6b602e29f0787ae70a37833cc681c9463b139f30a2fe5de5' ,

to : '0x6b4A7a46ad065b5fb142DEe92E9F4546982510fD' ,

transactionIndex : 2 ,

v : '0x29' ,

value : '0' ,

} ;

We can note here that the old raw transaction has added r and s fields, which is the digital signature of the transaction.

With this signature we can confirm that this is a transaction signed by address 0x937CDc3a7273269Fe43967E785D9e24D3C48C164 .

In fact, when interacting with Dapps, we often use Metamask or wallet applications that have been pre-programmed with the above functions, which makes it easy for users to access the application without having to understand too much. clear key, address and digital signature. Simply clicking OK or Cancel will suffice.

Conclude

Hopefully the article can help us understand more about ECDSA and its applications in blockchain, specifically here as Ethereum and Bitcoin.

And always keep your private key secure

Refer

Share the news now

Source : Viblo