Neuron people work like?
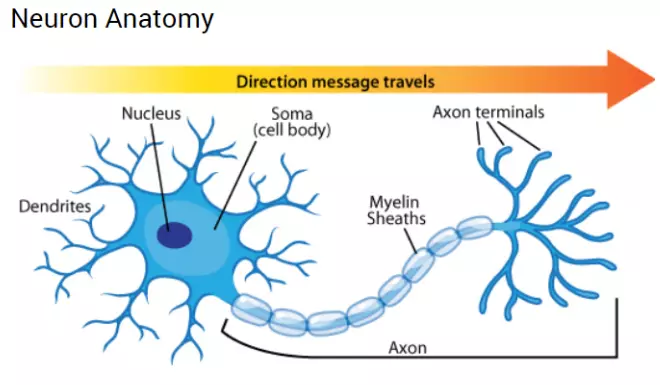Neurons are the basic unit of the nervous system and the most important part of the brain. Our brain consists of about 10 million neurons and each neuron is linked to 10,000 other neurons. In each neuron there is a nucleus (soma) containing the nucleus, the input signals via dendrites and axon output signals (axons) connected to other neurons. Simply understand, each neuron receives input data via branch fibers and transmits output data via axons, to the branch fibers of other neurons. Each neuron receives electrical impulses from other neurons via branch fibers. If these electrical impulses are large enough to activate the neuron, this signal passes through the axon to the branch fibers of other neurons. => Each neuron needs to decide whether to activate the neuron or not.
Deep learning, however, is just inspired by the brain and how it works, not mimicking its entire functions. Our main task is to use that model to solve the problems we need.
What is the general model of the Neural Network?
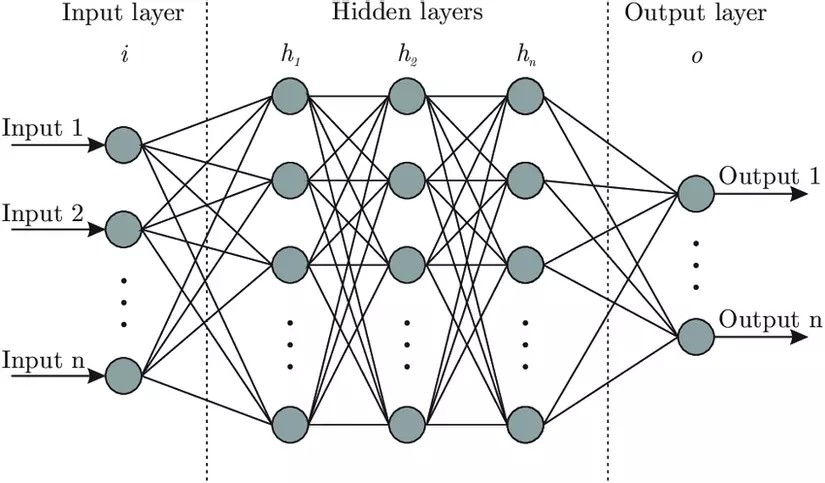The first layer is the input layer, the middle layer is called the hidden layer, the last layer is the output layer. A neural network is required to have an input layer and an output layer, hidden layers may or may not.
The circles in the layer are called nodes, or neural. These nodes are linked to all previous nodes and have their own factor w. Each node has its own bias b factor and then sums the weights with the previous input and applies the activation function to the nodes of the next layer.
What are the steps to setting up a deep learning problem?
- Data processing: Divide training, val, and test.
- Set model for machine learning.
- Set the loss function.
- Find parameters by optimizing the loss function, which tries to select the appropriate learning rate.
- Predict the test data by the model of the train.
What is the loss function?
The loss function, also known as the loss function, represents a relationship between y * (the predicted result of the model) and y (the actual value). For example, we have the following loss function: f (y) = (y * – y) ^ 2. At that time, people put in this loss function function is to optimize their model to the best, or also to evaluate the goodness of the model, y * (the predicted result of the model) as close to y ( is the actual value), the better. That is based on the loss function, then we can calculate the gradient descent to optimize the loss function as close to 0 as possible. (Currently I just present it so that you can understand, and the following section I will explain more about LAN TRANSMISSION for you to understand best).
What is the activation function, what does it mean?
The activation function simulates the rate of axon impulse transmission of a neuron, which is the nonlinear function applied to the output of neurons in the hidden layer of a network model (task is to normalize the output of neura) and be used as input data for the next floor. Biological neuron structure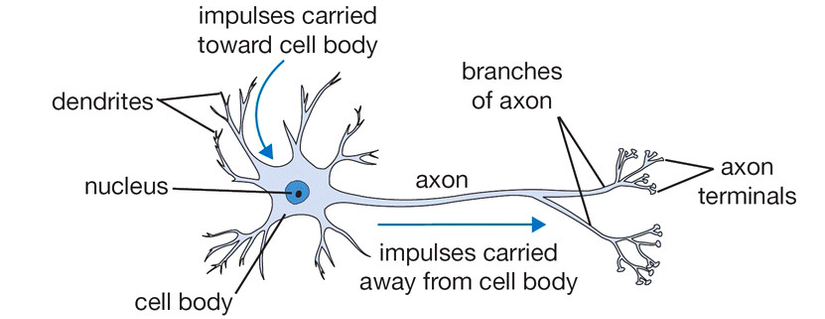 
Neuron structure in machine learning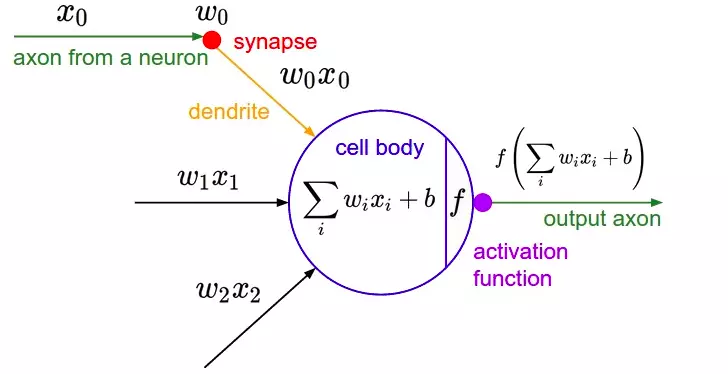 
As in biological models, nerve impulses are transmitted via axon at a certain rate. In the simulation machine learning model we build, activation functions will adjust this transfer rate. These functions are usually nonlinear functions.
What happens without these nonlinear functions?
Imagine that instead of applying a nonlinear function, we apply only one linear function to the output of each neuron. Because transformations are nonlinear, this is no different from adding another hidden layer because transformations are also simply multiplying the output by weights. With such simple calculations, neural networks will not be able to detect complex relationships of data (for example, stock predictions, image processing problems or transmitting problems). show semantics of sentences in the text). In other words, without activation functions, the predictability of neural networks will be limited and greatly reduced, the combination of activation functions between hidden layers is to help the model learn nonlinear relationships. Hidden complexity in data.
Why is the activation function non-linear? What happens if the linear activation function is used?
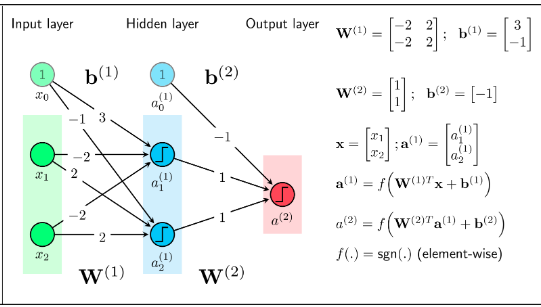The activation function must be nonlinear, because otherwise, many layers or one layer are the same. For example, with the two layers in Figure 2, if the activation function is a linear function (assuming f (s) = s) then both layers can be replaced by one with the coefficient matrix W = W1xW2 (temporarily omitted. bias coefficient)
Why are there so many layers and nodes in a hidden layer?
In the neural network we need a lot to handle many different tasks, each layer will perform a certain task, the output of this layer will be the input of the next layer. The number of layers is not limited, but for each specific problem, there will be different ways to select the layer to suit the problem. Usually with simple problems, the number of layers will be less, with more complex problems the number of layers will be more. You understand that each layer is a data processing to achieve a certain purpose.
We need multiple nodes in a hidden layer to make learning more effective. Assuming 2-way input, ie 2 nodes; The hidden layer has 1 node and the output layer has 1 node. then adjusting the weight of w1, w2 between the input node and the hidden layer will be limited for complicated problems, which will make learning bad.
Is the number of N nodes in the input layer the number of data points in the train set?
The answer is no. If the input layer has N nodes, then each sample (sample) in the train set will have N dimensions. In other words, each sample will be represented by a vector whose dimension is N. ==> N is not the number of data points in the train set.
Gradient descent
What is derivative?
Derivative is the change of function or the slope of a graph. Example: f (x) = x ^ 2 +1. Then f ‘(x) = 2x. Here, with x = 1 then f ‘(x) = 2, with x = 2 then f’ (x) = 4. We see that increasing x will increase f ‘(x), or the value of the function will increase. Another way to understand is that the function f (x) will increase as x increases from 1.
Partial derivatives ?
When the function has more variables 1. For example, f (x, y) = 2x + 3y then the concept of separate derivative will be born. Here, two concepts will be separated as derivative over x, and partial derivative over y. The derivative on x, will want to see how x affects how f (x, y). The derivative on y, will want to see how y affects f (x, y).
Gradient descent
So what is gradient descent? In essence, it is an algorithm that helps find the smallest value of the function, for example f (x) based on derivative, or f (x, y, …) based on the specific derivative of each variable. . For example, with f (x) = x ^ 2 +1 => f ‘(x) = 2x. We will perform the following steps to find the minimum value of f (x):
- Initialize the value x = x0 arbitrary
- Assign x = x – learning_rate * f ‘(x) (learning_rate is a non-negative constant, for example learning_rate = 0.001)
- Recalculate f (x): If f (x) is small enough, stop, otherwise continue to step 2
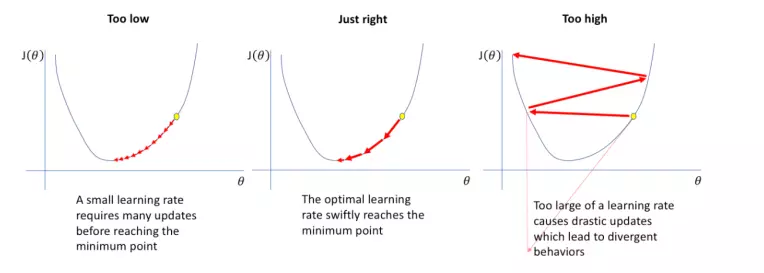
Choosing learning_rate is extremely important, there are 3 cases:
- If learning_rate is small: each time the function drops very little, it takes many times to perform step 2 to get the minimum value.
- If learning_rate is reasonable: after a moderate number of iterations of step 2, the function will reach a value small enough.
- If learning_rate is too large: it will cause overshoot (as shown in the picture on the right) and never reach the minimum value of the function.
What is Scalar, What is Vector, What is Matrix, What is Tensor?
- Scalar is a quantity that indicates the magnitude of something, or represents some value, without direction.
- Vector: When data represent a 1-dimensional form, it is called a vector.
- Matrix: When data is 2-dimensional, it is called a matrix, size is the number of rows * number of columns
- Tensor: When the data is more than 2, it will be called tensor, for example, the data has 3 dimensions.
I would like to stop here, I will continue to write part 2, hope you give me suggestions.
Refer
[1] Basic Deep Learning Book by Nguyen Thanh Tuan. Website: https://nttuan8.com/ [2] Basic Machine Learning https://machinelearningcoban.com/