Bloom filters are a probabilistic data structure, created in 1970 by Burton Howard, and are now widely used in information retrieval and storage. This article will describe how bloom filters work, then explain the trade-offs depending on individual purpose and ultimately some applications.

1. How Bloom Filters Work
1.1. Storage
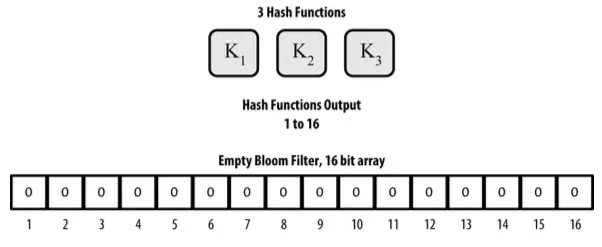
Bloom filters consist of an array of m binary elements (the value of each element is 0 or 1), and the k hashes are designed so that the output is an integer in the range 1 -> m.
Note: The hash function does not work randomly, with the same input, the hash function will also output the same output.
For example a bloom filter with m = 16 and k = 3:
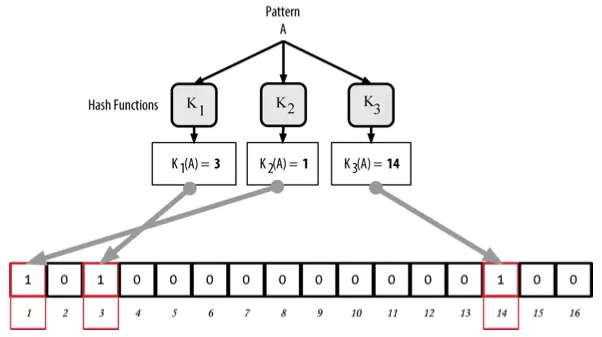
Initially, the elements in the array have a value of 0. To add an A record, A will go through the first hash function, and the element corresponding to the output of the hash function (in the range 1-> m) will converts to 1. Similarly, A will remove the remaining hashes.
Example of adding A record to bloom filter:
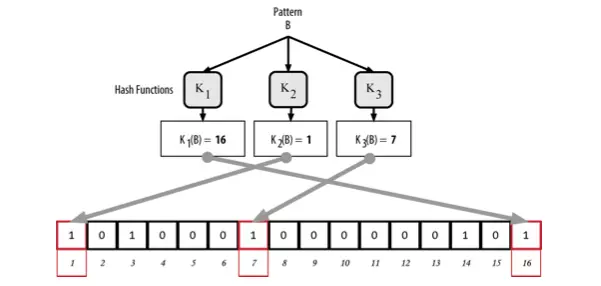
Similar to storing additional B records. It is worth noting: if the hash (when input B) returns the index of an element with a value of one, then that value remains the same. In essence, the more records that are stored, the greater the likelihood of duplicate elements, the lower the accuracy of the Bloom filter (discussed later). That is why Bloom filters are called probabilistic data structures.
An example of adding B record and the first element matches:
1.2. Search
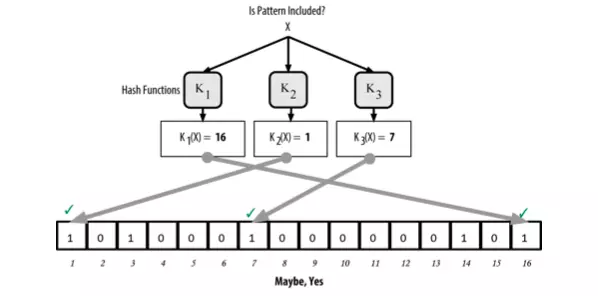
To check if an X record exists in bloom filters, it goes through each of the same hash functions above. The results are then collated against the storage array, if all the elements have the value 1 then that record is “probably” already stored. The reason “probably” is that because an element in the array with a value of 1 can be the result of storing many different records, the answer structure is still uncertain.
Example checks if X record is in bloom filter, the result returns “Maybe”.
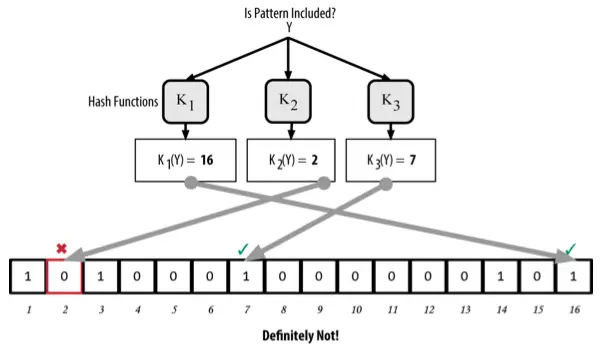
Conversely, if any element from the output of the hash has a value of 0, that means that the record is “Certainly not” in bloom filters.
Example checks if record Y is in bloom filter, the result returns “Sure not”
2. Trade-off
It can be claimed that accuracy depends on the number of records, the size of the storage array (m), and the number of hashes (k). In general, with increasing array size and number of hashes, bloom filters may store more records with greater precision, however there will be trade-offs. We try to see the following cases:
- When m is too small, the number of words with value 1 will take a large proportion, resulting in false positive results when searching for information. So increasing the array size can minimize this risk, but will take up more storage space.
- But when k is too small, the rate of false positive results is high. But if k is too large, it leads to slow, because a record has to go through too many hashes (time complexity o (k)).
Empirical evaluation of putting 10 million records in archival:

As can be seen from the graph, when the values of k and m are large, p (the probability of false positive result) will be small, but this makes Bloom filter slow. So, the best option here is to choose m = 100M and k = 5, since it has minimized the complexity of space and time.
3. Applications
- Google Bigtable, Apache HBase, Apache Cassandra, and Postgresql use bloom filters during searches to quickly determine if a instance is non-existent. Thereby, it can reduce costs and increase performance.
- Google Chrome uses Bloom Filter to identify malicious URLs. Any URL must be checked internally via the Bloom filter, and only those with a positive result will be “full checked” (and if it is true then it will send an alert to the user).
- Medium is used in the suggestion system to check if an article has been read by a user.
